Faites-vous attention, si le toit de la maison et la tente ont presque la même forme? Si vous regardez à nouveau, il semble qu'il se compose de 2 triangles à chaque extrémité, puis recouverts d'une couverture rectangulaire. Cette forme est également connue sous le nom de prisme triangulaire. On l'appelle ainsi parce que la base et le couvercle sont triangulaires. En géométrie, nous étudierons la définition et la formule des prismes triangulaires. A cette occasion, nous discuterons également de divers exemples du problème afin de pouvoir mieux comprendre ce matériel.
Un prisme est une forme qui a un couvercle et une base avec une forme congruente à n côtés, tandis que les côtés verticaux sont rectangulaires.
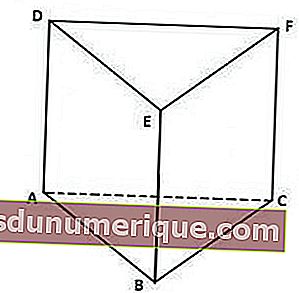
Les prismes triangulaires ont les caractéristiques suivantes:
A une base et un couvercle triangulaires congruents.
D'après l'image ci-dessus, le couvercle du prisme, à savoir le triangle DEF, a la même forme et la même taille que le triangle ABC que sa base.
Rectangle comme côté vertical.
Vous pouvez voir que le prisme ci-dessus est limité par trois rectangles de chaque côté de la verticale, à savoir les rectangles ACFD, BCFE et ABED.
A 5 côtés, 9 arêtes et 6 sommets.
Les 5 côtés d'un prisme triangulaire sont constitués de 1 côté de la base, 1 côté du couvercle et 3 côtés de la verticale. Alors que les 9 nervures se composent de 3 nervures verticales, 3 côtés de la base et 3 du côté du couvercle. De plus, les 6 sommets sont les points A, B, C, D, E et F.
Maintenant que nous connaissons les caractéristiques et aussi la signification d'un prisme triangulaire, il est temps pour nous d'apprendre à connaître les formules de prisme triangulaire et des exemples de leurs problèmes.
Formules de prisme triangulaire et exemples de problèmes
Il y aura 2 types de formules de prisme triangulaire que nous apprenons. La formule pour trouver le volume et la formule pour trouver la surface. Les formules sont comme ceci:
Le volume
Pour le volume, nous utiliserons la formule:
V = aire de la base × hauteur
ou
V = (½ x a x h) × hauteur du prisme
Donc, pour mieux comprendre cela, regardons un exemple de ce problème:
Un prisme mesure 10 cm de haut. La base du prisme a la forme d'un triangle rectangle avec des longueurs latérales de 4 cm et 3 cm, respectivement. Quel est le volume de ce prisme triangulaire?
Solution:
Ici, il suffit de brancher les nombres connus dans une formule comme celle-ci:
V = (½ x a x h) × hauteur du prisme
V = (½ x 4 x 3) × 10
V = 6 × 10
V = 60 cm 3
Superficie
Pour calculer la surface d'un prisme triangulaire, nous utiliserons une formule comme celle-ci:
L = (2 x aire de la base) + (aire de tous les côtés perpendiculaires)
si le triangle est équilatéral, vous pouvez utiliser la formule:
L = (2 x aire de la base) + (3 x aire d'un côté de la verticale)
Ou cela pourrait être la formule:
L = (2 x aire de la base) + (périmètre de la base x hauteur du prisme)
Regardons un exemple de ce problème pour voir comment cette formule est appliquée. Voici un exemple de problème:
Il y a un prisme triangulaire équilatéral qui a une hauteur de 12 cm, une longueur de côté de 5 cm et une hauteur de 8 cm. Alors quelle est la surface de ce prisme triangulaire?
Solution:
Pour trouver la surface, nous utilisons simplement la formule de la surface d'un prisme triangulaire comme ceci:
L = (2 x aire de la base) + (3 x aire d'un plan vertical)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 cm 2
Voilà donc les différentes formules de prisme triangulaire que vous devez connaître, ainsi que quelques exemples de problèmes. Si vous êtes toujours confus, vous pouvez demander dans la colonne des commentaires, ou vous pouvez essayer Smart Class, la plate-forme de tutorat en ligne de confiance dans World.









