Les pneus de voiture et de moto sont circulaires, les plaques sont également circulaires, les bouchons de bouteilles sont également circulaires et même de nombreuses horloges murales ont une forme circulaire. Cette construction plate que nous rencontrons souvent dans la vie quotidienne pour que la forme soit familière. Il est maintenant temps pour vous d'apprendre à connaître cette forme plate, sa définition et la formule de la circonférence d'un cercle. Il existe également des exemples de questions qui peuvent vous aider à mieux comprendre cela. Allez, commençons.
Un cercle est une forme où tous les points du cercle sont à la même distance du centre. La distance entre n'importe quel point du cercle et le centre s'appelle le rayon.
Un cercle comprend plusieurs parties, telles que:
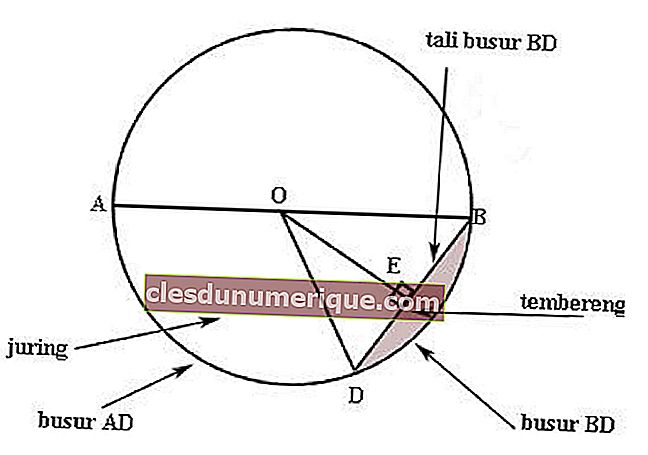
Source de l'image: formularumus.com
Point central (O)
Est le milieu du cercle, où la distance entre le point et n'importe quel point du cercle est toujours constante.
Les doigts
Est une ligne droite reliant le point central au point du cercle. Le rayon est la distance entre le point central et le point sur le cercle.
Corde d'arc
Une ligne droite dans un cercle qui coupe le cercle en deux points différents.
Arc
Est une ligne courbe dans le cercle.
Circonférence
Est l'arc le plus long du cercle.
Diamètre
La plus longue chaîne passant par le centre est appelée le diamètre. La longueur du diamètre est le double du rayon. Ce diamètre divise le cercle en deux parties égales.
Apothème
La ligne la plus courte entre la corde et le centre du cercle.
Juring
L'aire d'un cercle délimité par un arc et deux rayons.
Tesson de poterie
La zone du cercle délimitée par un arc avec une corde d'arc.
En dehors de ces parties, un cercle a également les propriétés suivantes:
- Avoir un côté
- Il n'a pas de sommets
- Un cercle a une symétrie de pliage infinie
- Un cercle a une symétrie de rotation infinie
- La distance du centre à n'importe quel point du cercle est toujours la même
Étudions maintenant la formule de calcul du périmètre d'un cercle.
Formule de circonférence
La circonférence d'un cercle est la distance d'un point sur un cercle en un tour complet et retour au point d'origine. Calculer la circonférence d'un cercle n'est en fait pas une chose difficile. Pour calculer la circonférence d'un cercle, vous pouvez utiliser deux méthodes. Si donné le rayon ou si le diamètre est connu.
La deuxième formule est comme ceci:
Rayon connu:
C = 2 x π xr
Diamètre connu:
C = π xd
π = 22/7 nous utiliserons si le rayon (r) ou le diamètre (d) est un multiple de 7 ou peut être divisé par 7
π = 3,14 nous utiliserons si le rayon (r) ou le diamètre (d) n'est pas un multiple de 7 ou ne peut être divisé par 7
Regardons maintenant un exemple de ce problème:
1. Un cercle a un rayon de 7 cm. Quelle est la circonférence du cercle?
Solution:
Périmètre = π x 2 x rayon, alors
K = 22/7 x 2 x 7 = 44 cm
2. Un étang à poissons circulaire d'un diamètre de 10 m, quelle est la circonférence de l'étang à poissons?
Solution:
Périmètre = π xd, alors
K = 3,14 x 10 = 31,4 m
Voilà donc une petite discussion sur la formule de la circonférence d'un cercle, si vous avez des questions à ce sujet, n'hésitez pas à l'écrire dans la colonne des commentaires. N'oubliez pas de le partager aussi!