Si vous étudiez les mathématiques, vous devez avoir entendu ou étudié la trigonométrie. Eh bien, la trigonométrie est une branche des mathématiques qui étudie la relation entre l'angle et la longueur des côtés d'un triangle, comme le sinus, le cosinus et la tangente. Prise à la lettre, la trigonométrie vient du grec, à savoir trigonon qui signifie «trois angles» et métron, signifiant «mesurer». Comme pour divers matériaux en mathématiques, il existe des formules trigonométriques que vous devez connaître.
A cette occasion, nous tenterons de comprendre différents types de formules ainsi que des exemples de leurs problèmes.
Formules trigonométriques
Le concept de trigonométrie est un concept important dans les triangles. Les valeurs trigonométriques sont formulées sur la base du rapport des longueurs des côtés d'un triangle rectangle. Il existe six valeurs de rapport trigonométrique, à savoir sinus (sin), cosinus (cos), tangente (tan), cosécante (cosec), sécante (sec) et cotangente (cot). Les six types de valeurs trigonométriques peuvent être déterminés en comparant les longueurs des côtés avec certaines règles.
Les utilisations de la trigonométrie sont nombreuses, allant de l'astronomie, de la géographie, de la théorie musicale, de l'acoustique, de l'analyse optique des marchés financiers, de l'électronique, de la théorie des probabilités, des statistiques, de la biologie, de l'imagerie médicale, de la pharmacie, de la chimie et bien d'autres.
Le moment est venu pour nous d'apprendre à connaître les différentes formules trigonométriques de cette leçon.
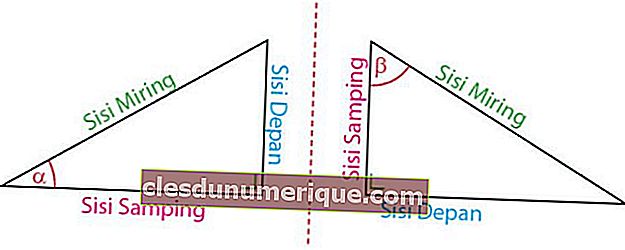
Source de l'image: idschool.net
En fonction de son emplacement par rapport à l'angle, les côtés du triangle - coude sont divisés en trois types, à savoir le côté avant, le côté latéral et l'hypoténuse. La face avant est la face tournée vers le coin. Le côté est du côté du coin. Le côté incliné est toujours devant l'angle de 90o.
Eh bien, les trois principales fonctions trigonométriques sont les fonctions sin, cos et tan. La définition des trois fonctions basées sur les côtés et les angles d'un triangle rectangle peut être vue dans la figure et l'équation ci-dessous.
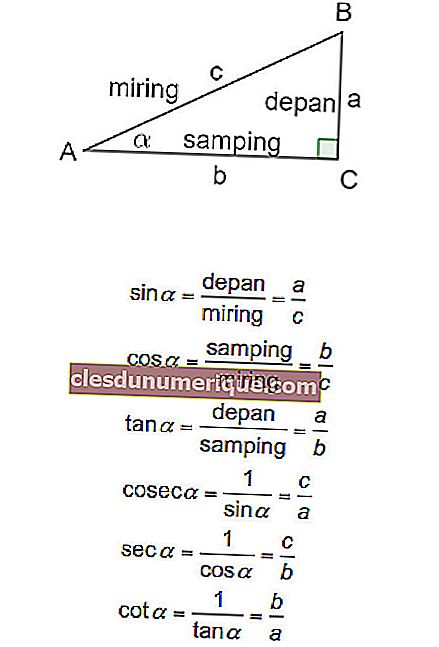
Maintenant, spécifiquement pour les angles spéciaux, les valeurs trigonométriques sont les suivantes:
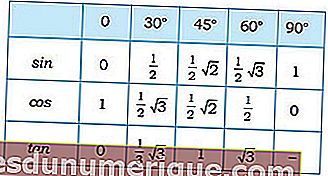
Source de l'image: madematics.net
Comparaison trigonométrique d'angle corrélé
Le rapport trigonométrique de l'angle associé est l'extension de la valeur de déclenchement de base qui est déterminée à partir de l'angle du triangle rectangle. L'angle d'un triangle rectangle n'est que dans le quadrant I car il s'agit d'un angle aigu dont la taille est de 0 ° à 90 °.
L'angle central du cercle est compris entre 0 ° et 360 °. L'angle est divisé en 4 quadrants, chaque quadrant a une portée de 90 °.
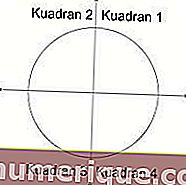
Source de l'image: studiobelajar.com
- Le quadrant 1 a un angle compris entre 0 ° et 90 °. Toutes les valeurs du rapport trigonométrique sont positives dans ce quadrant.
- Le quadrant 2 a un angle compris entre 90 ° et 180 °. Dans ce quadrant, seules les valeurs sinus et cosécante sont positives.
- Le quadrant 3 a un angle compris entre 180 ° et 270 °. Dans ce quadrant, seules les tangentes et cotangentes sont positives.
- Le quadrant 4 a un angle compris entre 270 ° et 360 °. Dans ce quadrant, seuls le cosinus et la sécante sont positifs.
Identité trigonométrique
Le théorème de Pythagore, à savoir a2 + b2 = c2, est à la base de la préparation des identités trigonométriques. Les identités trigonométriques expriment la relation entre une fonction trigonométrique et d'autres fonctions trigonométriques.
La somme du sinus au carré et du cosinus au carré est égale à un. Si les deux côtés sont divisés par le cosinus au carré, un plus la tangente au carré est égal à la sécante au carré. De même, si les deux côtés sont divisés par le sinus au carré, nous pouvons obtenir un plus la cotangente au carré égale le cosecan au carré.
Voici la formule d'identité:
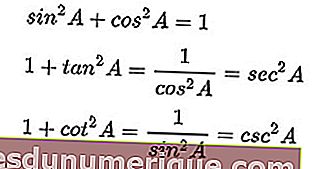
Source de l'image: wikipedia.org
Diverses autres formules
Il y a une autre formule que vous devriez connaître, à savoir:
La formule de la somme et de la différence des angles:
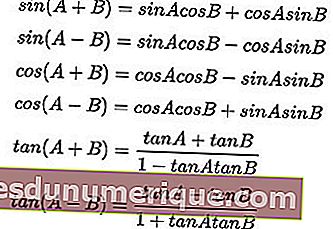
Formules de multiplication trigonométriques:
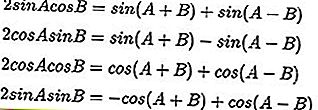
Formules de somme trigonométrique et de différence:
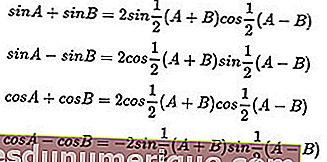
Exemples de problèmes déclencheurs
Trouvez la valeur de 2 cos 75 ° cos 15 °:
Solution:
Sur la base des informations contenues dans le problème, nous pouvons voir que le problème ci-dessus inclut la multiplication trigonométrique. Utilisez la formule de multiplication pour cos décrite ci-dessus, qui est 2 cos A cos B = cos (A + B) + cos (A - B).
Répondre:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75-15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
C'est un ensemble de formules et de problèmes trigonométriques que vous pouvez apprendre et comprendre. Pour mieux le comprendre, vous pouvez essayer PROBLEM, une solution pondérée, complète et en ligne pour pratiquer des questions conformément au dernier programme de Smart Class. À partir du niveau élémentaire, du premier cycle du secondaire au secondaire avec diverses matières telles que les mathématiques, la physique, la chimie et autres. Ici, vous pouvez apprendre différents types de formules avec des exemples de problèmes,
Allez, qu'attendez-vous! Essayons dès maintenant les exercices PROBLÈME dans Smart Class.









