Qui aime la glace? De plus, la crème glacée qui utilise des cônes. C'est vraiment bon, c'est froid et sucré aussi. Alors, est-ce que quelqu'un s'est déjà demandé combien de volume de glace devrait être rempli dans un cône jusqu'à ce qu'il soit plein? Quelqu'un sait-il calculer le volume de cette glace? Wow, sinon, c'est l'occasion pour vous d'apprendre la formule du volume d'un cône et aussi comment le calculer.
Mais, avant de plonger dans la formule du volume d'un cône et aussi comment le trouver, apprenons à savoir ce qu'est un cône. Le cône est l'un des espaces latéraux incurvés. Il a une base circulaire et une couverture qui relie la base et le point supérieur.
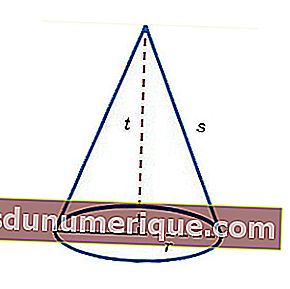
Le cône a également 3 tailles importantes que nous utiliserons pour calculer son volume, à savoir:
1. Radius Cone
La base du cône est un cercle. Le rayon ou rayon du cône est la distance entre le point central et le point sur le cercle de base. Le diamètre de la base conique est un segment qui relie deux points sur le cercle de base et à travers le point central. Dans un cercle, le diamètre du cercle est égal à deux fois le rayon du cercle.
2. Hauteur du cône
Est la distance entre le centre de la base et le sommet du cône. Si nous créons un segment de ligne qui relie le centre de la base et le sommet, alors un segment qui est perpendiculaire au plan de la base est obtenu. La longueur de ce segment est également la hauteur du cône.
3. Couverture de cône
La couverture de cône est un côté incurvé, s'enroulant autour du cône. Il est situé entre la base et le point haut. Dans la couverture des cônes se trouvent les lignes des peintres. Une ligne de peintre est une ligne qui représente la courtepointe la plus externe d'un cône. La ligne du peintre, la hauteur du cône et le rayon du cône forment un triangle rectangle.
Outre les éléments ci-dessus, il faut également connaître les caractéristiques d'une forme de cône, à savoir:
- Le cône a un côté.
- Le cône a un sommet.
- Les cônes n'ont pas de côtes.
- Les cônes ont des filets en forme de cercles et de grilles circulaires.
Passons maintenant à la formule du volume d'un cône et comment le calculer.
Formule de volume de cône
Pour calculer le volume d'un cône, nous utiliserons cette formule unique:
V = 1/3 x π x r2 xt
Information:
v = volume du cône
t = hauteur du cône
r = le rayon de la base du cône
Nous utiliserons π = 22/7 si le rayon (r) ou le diamètre (d) sont un multiple de 7 ou divisible par 7.
Nous utiliserons π = 3,14 si le rayon (r) ou le diamètre (d) ne sont pas un multiple de 7 ou ne sont pas divisibles par 7.
Regardons un exemple de ce problème pour mieux comprendre comment trouver le volume d'un cône.
Question:
Un cône a un rayon de base de 10 cm et une hauteur de 20 cm. Quel est le volume du cône?
Solution:
Nous avons juste besoin d'entrer les nombres dans la formule, comme ceci:
V = 1/3 x π x r2 xt
V = 1/3 x 3,14 x 10 cm2 x 20 cm
V = 2 093,33 cm3
Si vous pensez que vous avez encore besoin de plus de questions pour comprendre ce matériel, vous pouvez profiter des produits PROB de Smart Class. Dans ce produit, il existe différents types de questions pratiques pour vous permettre d'apprendre à être plus stable face aux examens. Comprend des problèmes sur les cônes. Il existe également une fonction QUESTION accessible gratuitement et permettant de répondre à des questions sur des questions ou du matériel qui n'ont pas été maîtrisés. Vos questions sont répondues immédiatement par des enseignants et des mentors certifiés.
Voilà donc une petite discussion sur la formule de volume d'un cône que vous devriez connaître. Si vous êtes toujours confus, écrivez votre question dans la colonne des commentaires.









