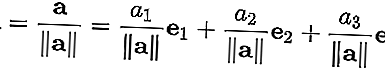Les vecteurs en mathématiques et en physique peuvent être définis comme des objets géométriques qui ont une magnitude et une direction. Le vecteur est représenté par une flèche, où la base de la flèche montre un point d'accrochage (point de départ) d'un vecteur, la longueur de la flèche indique la taille ou la valeur du vecteur (plus la flèche est longue, plus la valeur ou la valeur du vecteur est élevée, et vice versa) , tandis que la flèche indique la direction du vecteur.
En écriture, si le vecteur commence au point A et se termine au point B, alors il peut être écrit dans une petite lettre au-dessus de laquelle il y a une ligne / flèche comme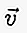 
ou 
ou 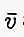aussi:
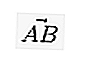
Types de vecteurs
Le vecteur en mathématiques est divisé en 4 types, dont:
Vecteur de position
Un vecteur dont le point de départ est à 0 (0,0) et sa fin est A (a1, a2).
Zéro vecteur
"Vecteur zéro" ( vecteur nul ou vecteur nul ) est un vecteur dont la longueur est "zéro". L'écriture dans les coordonnées de ce vecteur est (0,0,0), et reçoit généralement le symbole 
, ou 0 . Ce vecteur diffère des autres vecteurs en ce qu'il ne peut pas être normalisé (c'est-à-dire qu'aucun vecteur unitaire n'est un multiple du vecteur nul). La somme des vecteurs nuls avec n'importe quel vecteur a est a (c'est-à-dire 0 + a = a ).
Le vecteur zéro n'a pas de direction vectorielle claire.
Vecteur d'unité
est un vecteur de longueur "un". Les vecteurs unitaires ne sont généralement utilisés que pour indiquer la direction. Un vecteur de n'importe quelle longueur peut être divisé par la longueur pour obtenir le vecteur unitaire. C'est ce qu'on appelle la "normalisation" d'un vecteur. Un vecteur unitaire est souvent indiqué par un «cap» sur le «a» minuscule comme dans - .
Pour normaliser un vecteur a = [ a 1 , a 2 , a 3 ], divisez le vecteur par sa longueur || a ||. Donc:
Vecteur de base
Un vecteur unitaire perpendiculaire l'un à l'autre. Dans un espace à deux dimensions, le vecteur ( R 2 ) a deux vecteurs de base, à savoir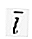 
= (1, 0) et 
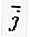= (0, 1).
Similitude de deux vecteurs
On dit que deux vecteurs sont identiques s'ils ont la même longueur et la même direction
Un alignement de deux vecteurs
Deux vecteurs sont dits parallèles (parallèles) si la ligne représentant les deux vecteurs est parallèle.
Opérations vectorielles
Multiplication scalaire
Un vecteur peut être multiplié par un scalaire qui se traduit également par un vecteur, le vecteur résultant est:
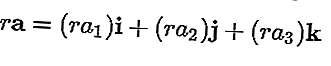
Addition de vecteur et soustraction de vecteur
Par exemple, les vecteurs a = a 1 i + a 2 j + a 3 k et b = b 1 i + b 2 j + b 3 k
Le résultat d'un plus b est: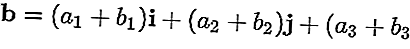 
la réduction vectorielle s'applique également en remplaçant le signe + par un signe -
