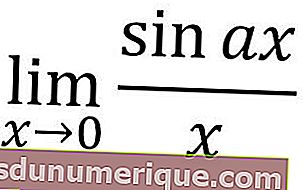La limite de la fonction trig est définie comme la valeur la plus proche d'un angle dans la fonction trig. Ce calcul peut être substitué comme la limite d'une fonction algébrique, mais avec une fonction trigonométrique qui doit d'abord être modifiée.
La fonction trigonométrique doit être convertie en une identité trigonométrique pour une limite indéfinie, qui est une limite qui, si elle est substituée, sera 0. En outre, il existe également un moyen de calculer une limite indéfinie sans utiliser l'identité trigonométrique, mais en utilisant le théorème de limite trigonométrique. D'autres utilisent simultanément l'identité et le théorème.
Pour déterminer la valeur limite des fonctions trigonométriques, il existe différentes manières qui peuvent être utilisées, à savoir les méthodes numériques, la substitution, la factorisation, les temps des pairs et les dérivés.
(Lire aussi: Mesurer la visibilité à l'aide de formules trigonométriques)
Mais en fonction de la valeur, nous pouvons diviser cette formule en deux, c'est-à-dire celles qui sont proches du nombre et proches de zéro.
X Approche d'un nombre
Si nous avons la limite de la fonction trigonométrique dont x s'approche du nombre c, nous pouvons déterminer sa valeur en substituant c dans la fonction trig. Les formules sont les suivantes.

X proche de zéro
Si le x d'une limite de fonction trigonométrique s'approche de zéro, nous pouvons utiliser les formules ci-dessous.

Si après avoir substitué la valeur de x dans la fonction trig la forme indéfinie est 0/0 ∞ / ∞, alors pour déterminer la valeur limite de la fonction trigonométrique, vous pouvez utiliser la règle de L'Hospital, à savoir
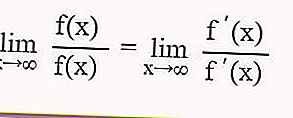
Intuition Compréhension des limites des fonctions de déclenchement
Comprendre intuitivement la limite d'une fonction trigonométrique équivaut à la limite d'une fonction algébrique. La limite de la fonction trig existe si et seulement si la limite gauche et la limite droite existent et la limite gauche est égale à la limite droite.