Le cercle est un ensemble de points équidistants d'un point. Les coordonnées de ces points sont déterminées par la disposition des équations circulaires. Ceci est déterminé en fonction de la longueur du rayon et des coordonnées du centre du cercle.
Dans l'image ci-dessus, nous pouvons conclure que OP = OQ. Le point O est appelé le centre du cercle, tandis que OP et OQ sont les rayons. Prenons l'exemple suivant.
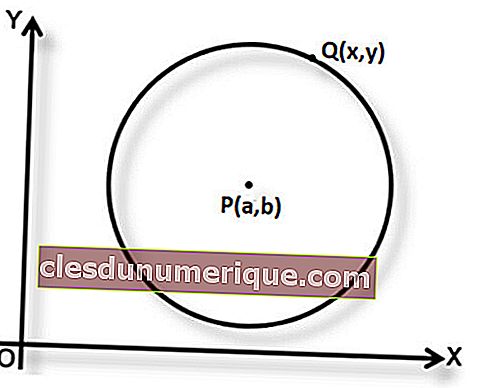
P (a, b) est le centre du cercle et la longueur du rayon est r. Si Q (x, y) est un point situé sur le cercle, d'après la définition du cercle, on peut conclure que PQ = r. À partir de là, nous pouvons formuler l'équation du cercle avec P (a, b) comme centre et r comme rayon.
√ (x - a) 2 + (y - b) 2 = r
(x - a) 2 + (y - b) 2 = r2
Travaillons sur un exemple de problème ci-dessous.
Trouvez l'équation du cercle dont le centre est au point (-5,4) dont le rayon est 7!
À partir de ces déclarations, nous savons que a = -5, b = 4 et r = 7. Si nous les connectons à l'équation, nous obtenons la réponse suivante.
(x - (-5)) 2 + (y - 4) 2 = 72
(x + 5) 2 + (y - 4) 2 = 49
Que diriez-vous d'un cercle dont la coordonnée centrale est à P (0,0)? L'équation du cercle est la suivante.
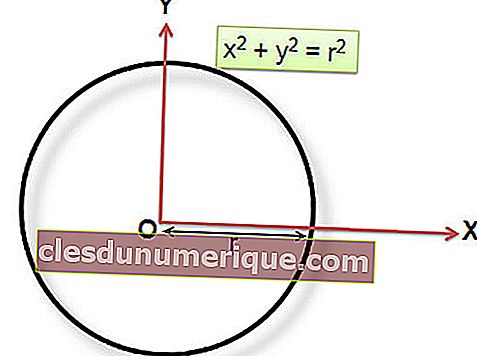
La forme générale de l'équation circulaire peut être exprimée sous les formes suivantes.
(x - a) 2 + (y - b) 2 = r2, ou
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, ou
X2 + y2 + Px + Qy + S = 0, où P = -2a, Q = -2b et S = a2 + b2 - r2
Conditions de détermination de l'équation d'un cercle
L'équation circulaire contient trois variables arbitraires. L'équation du cercle peut être déterminée si les valeurs des trois variables sont connues. Pour connaître les valeurs de ces trois variables, l'une des conditions suivantes doit être remplie:
- Les coordonnées des trois points du cercle sont connues.
- Les coordonnées de deux points sur le cercle reliés par le diamètre du cercle sont connues.
- Les coordonnées du point central et les coordonnées du point sur le cercle sont connues.









