En mathématiques, un modèle numérique est un arrangement de plusieurs nombres qui forment un certain modèle. Plusieurs types de modèles de nombres incluent les modèles pairs, impairs, arithmétiques et géométriques. Aujourd'hui, nous allons discuter de deux types de motifs numériques, à savoir la ligne géométrique et les séries géométriques.
Une ligne géométrique est une séquence de nombres composée de termes qui ont des proportions fixes. Le premier terme de la suite géométrique est désigné par a. Le rapport ou la comparaison entre deux termes est noté r.
Les lignes géométriques peuvent être formulées comme suit.
a, ar, ar2, ar3,…, arn-
a = le premier terme de la suite géométrique
r = le rapport entre les termes
n = séquence de termes
Pour déterminer la valeur du nième terme ou ratio, nous pouvons utiliser la formule suivante.
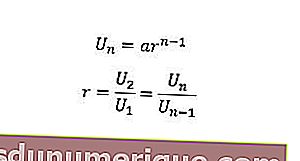
U n = le nième terme
Travaillons sur un exemple de problème ci-dessous.
Étant donné une séquence géométrique 3, 9, 27, 81, 243. Sur cette base, déterminez alors le rapport de la séquence géométrique!
Nous connaissons U 1 = 3 et U 2 = 9, de sorte que si nous les mettons dans la formule, nous obtiendrons le résultat suivant.
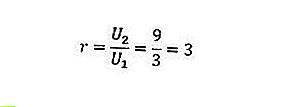
Ainsi, le rapport ou la comparaison de la séquence géométrique ci-dessus est de 3.
(Lire aussi: Logique mathématique, de la négation à la biimplication)
Pendant ce temps, une série géométrique est la somme des termes dans une séquence géométrique. Une série géométrique peut être désignée par S n qui signifie le nombre des n premiers termes de la suite géométrique.
La série géométrique peut être formulée comme suit.

a = le premier terme de la suite géométrique
r = le rapport entre les termes
n = la séquence des derniers termes ajoutés
U n = le nième terme
Travaillons sur un exemple de problème ci-dessous.
Étant donné qu'une série géométrique avec le premier terme est 6 et le quatrième terme est 48, alors la somme des six premiers termes est…?
On sait que a = 6 et U 4 = 48. Si l'on branche la formule, le résultat sera le suivant.
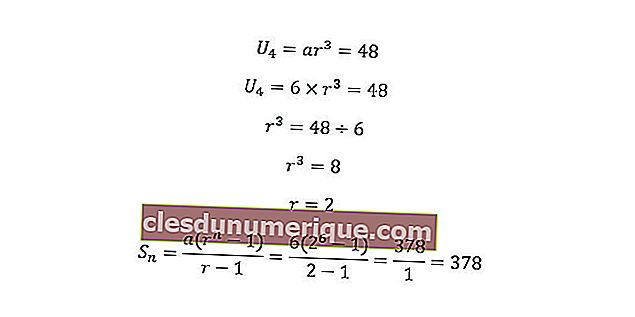
Ainsi, la somme des 6 premiers termes de la série ci-dessus est de 378.









