Si vous faites attention, un trapèze est une forme qui est une combinaison d'autres formes, à savoir des triangles, plus précisément des triangles rectangles et des rectangles ou des carrés. Le trapèze a également un autre nom, à savoir le trapèze. A cette occasion, nous étudierons la définition ainsi que la formule de l'aire d'un trapèze et des exemples de ses problèmes. Faisons connaissance avec cette forme plate.
Un trapèze est une forme formée de quatre côtés, dont deux sont parallèles l'un à l'autre mais pas de la même longueur. Inclus dans le type de forme rectangulaire avec une symétrie tournante. Nous pouvons en conclure que le trapèze a les propriétés suivantes:
- Y compris le type de forme rectangulaire.
- A une paire de côtés parallèles.
- A une seule symétrie rotative.
- A une symétrie de pli dans un trapèze isocèle.
Le trapèze lui-même se compose de trois types, à savoir:
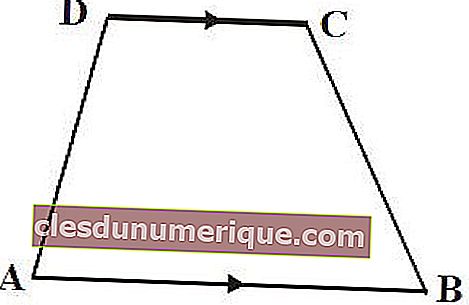
Tout trapèze, qui est un trapèze où les quatre côtés ne sont pas de la même longueur et n'ont pas d'angle droit. Ce trapèze n'a pas de symétrie de pli et seulement 1 symétrie de rotation.
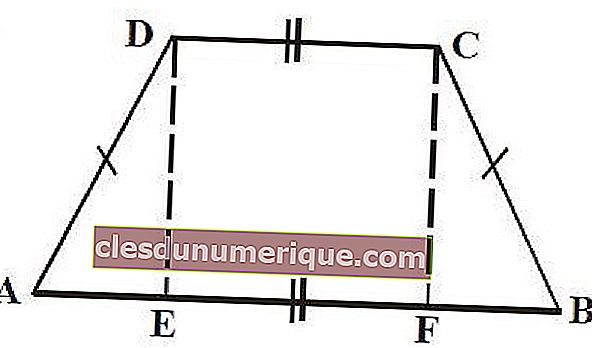
Un trapèze isocèle, qui est un trapèze qui a une paire de côtés égaux, a 1 symétrie de pli et 1 symétrie de rotation.
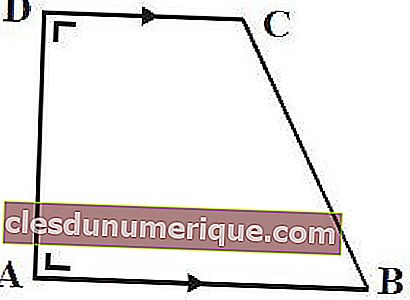
Le trapèze droit , est un type de trapèze à deux angles droits. Ce trapèze n'a pas de symétrie de pli et une seule symétrie de rotation.
Eh bien, nous savons déjà ce qu'est un trapèze et aussi ses propriétés, ainsi que les différents types. Maintenant, commençons à apprendre la formule de l'aire d'un trapèze.
Formule d'aire trapézoïdale et exemples de problèmes
Dans l'activité de calcul de l'aire d'une forme trapézoïdale, nous utiliserons cette formule unique:
Aire = ½ × longueurs totales des côtés parallèles × hauteur
Sur la base de cette formule, nous pouvons calculer l'aire d'un trapèze. Pour être en mesure de mieux comprendre cette formule, regardons un exemple de ce problème.
Exemple de problèmes:
Il y a un trapèze avec des côtés parallèles de 20 cm et 12 cm respectivement et une hauteur de 6 cm. Quelle est l'aire du trapèze?
Solution:
Avec la formule que nous avons apprise précédemment, alors
W = ½ × la somme des longueurs du côté × la hauteur
L = ½ × (20 + 12) × 6
L = ½ × 32 × 6
L = 96 cm²
Comment? Comprenez-vous mieux? Si cela manque encore, vous pouvez essayer d'étudier en classe intelligente. Une ligne plate - forme d'apprentissage qui a de nombreux avantages. Avec une plate-forme numérique à 360 ° accessible par les élèves, les enseignants et les parents pendant le processus d'apprentissage, ainsi qu'un système intégré, soutiendra le développement de l'apprentissage des élèves. Dans Smart Class, vous pouvez apprendre une variété de sujets, y compris les mathématiques et même les formes.
Il y a 2 packages fournis, à savoir le programme régulier et MBG. Regular est un programme Smart Class ordinaire qui offre diverses installations et avantages pour les activités d'apprentissage en ligne .
MBG, qui signifie Garantie de remboursement, est un programme Smart Class qui offre des remboursements s'il n'y a pas d'augmentation des notes des étudiants, bien sûr sous certaines conditions.
Si vous souhaitez en savoir plus et poser d'autres questions sur ce matériel, vous pouvez essayer le produit PROBLEM de Smart Class. Il existe différents types de questions pratiques à apprendre, afin que vous puissiez vous entraîner avec la meilleure variété de questions. Il existe également une fonction DEMANDE qui peut être consultée GRATUITEMENT pour vous aider à répondre à diverses questions sur des questions ou du matériel qui n'ont pas été maîtrisés.
C'est la discussion sur la formule d'aire d'un trapèze que vous devriez connaître. S'il y a quelque chose que vous ne savez pas, veuillez noter votre question dans la colonne des commentaires.









