Juste pour que vous le sachiez, les relations existent aussi en mathématiques, vous savez. Des relations existent dans le matériau concernant les ensembles. Les relations sont des règles qui connectent les membres d'un ensemble avec d'autres membres de l'ensemble. La relation de l'ensemble A à l'ensemble B relie les membres de l'ensemble A aux membres de l'ensemble B. Dans cette opportunité, nous découvrirons des exemples de relations et de leurs propriétés, ainsi que divers exemples de problèmes qui peuvent vous aider à mieux comprendre ce matériel.
Exemples de relations et leur nature
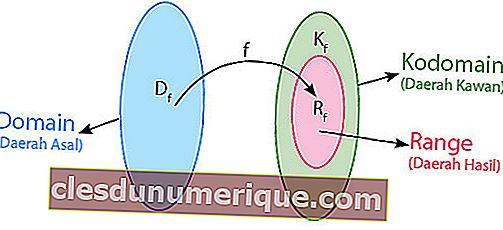
La relation peut être définie comme une règle qui relie les membres de la zone d'origine (domaine) et les membres d'une zone amie (codomaine). Dans une relation, il n'y a pas de règles spéciales à respecter pour associer les membres de l'association régionale aux membres des régions amies.
source: idschool.net
Chaque membre de l'association régionale d'origine peut avoir plus d'un partenaire ou ne pas avoir de partenaire du tout. La relation de deux ensembles peut être exprimée de trois manières, à savoir:
- Diagramme de flèche
- Diagramme cartésien.
- L'ensemble des paires consécutives
Ce qui suit est une explication supplémentaire des trois façons:
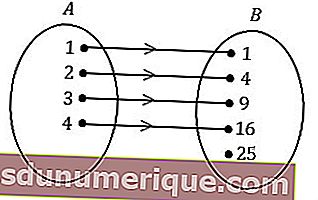
Graphiques fléchés
Les graphiques fléchés sont le moyen le plus simple d'exprimer une relation. Ce diagramme formera un modèle de relation sous la forme d'une flèche qui montre la relation entre les membres de l'ensemble A et les membres de l'ensemble B.
Source: maretong.com
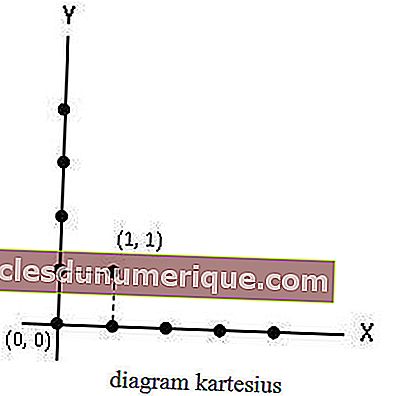
Diagramme cartésien
Le diagramme cartésien est un diagramme composé d'un axe X et d'un axe Y. Dans un diagramme cartésien, les membres de l'ensemble A sont situés sur l'axe X, tandis que les membres de l'ensemble B sont situés sur l'axe Y. Les relations qui relient l'ensemble A à B sont indiquées par des points ou des points.
Ensemble de paires consécutives
Une relation qui relie un ensemble à un autre ensemble peut être représentée sous la forme d'un ensemble de paires ordonnées. La façon d'écrire est que les membres de l'ensemble A sont écrits en premier, tandis que les membres de l'ensemble B qui sont les paires sont écrits en second.
Exemples comme celui-ci:
A = set du monde, Japon, Corée, France
Set B = Tokyo, Paris, Jakarta, Séoul
Déterminez l'ensemble ordonné de paires par pays et par capitale.
Répondre:
{(Monde, Jakarta), (Japon, Tokyo), (Corée, Séoul), (France, Paris)}
Fonction
Une fonction ou un mappage est une relation spéciale entre l'ensemble A et l'ensemble B, avec la règle selon laquelle chaque membre de l'ensemble A correspond exactement à un membre de l'ensemble B.
Le résultat du mappage d'un domaine à un autre est appelé plage de fonctions ou zone de résultats. À l'instar des relations, les fonctions peuvent également être représentées sous forme de diagrammes fléchés, de paires ordonnées et de diagrammes cartésiens.
Source: rumushitung.com
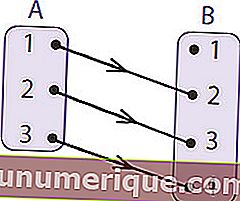
Pour mieux comprendre, considérez l'image ci-dessus. L'ensemble A ou zone d'origine est appelé le domaine. L'ensemble B qui est une zone amie est appelé un codomaine. Le membre de la zone conviviale résultant du mappage est appelé zone de rendement ou plage de fonctions. Ainsi, à partir du diagramme fléché ci-dessus, on peut conclure que
- Le domaine (D f) est A = {1,2,3}
- Le codomaine est B = {1,2,3,4}
- Plage / résultat (R f) est = {2,3,4}
Les fonctions peuvent être désignées par des lettres minuscules telles que f, g, h, i, etc. La fonction f associe l'ensemble A à l'ensemble B, alors elle peut être désignée par f (x): A → B.
Un exemple est la fonction f qui mappe A à B avec la règle f: x → 2x + 2. D'après la notation de la fonction, x est un membre du domaine. La fonction x → 2x + 2 signifie que la fonction f mappe x à 2x + 2. Ainsi, l'aire de x par la fonction f est 2x + 2. Vous pouvez donc la désigner par f (x) = 2x +2.
Si la fonction f: x → ax + b avec x est un membre du domaine f, alors la formule de la fonction f est
f (x) = ax + b
Exemple de problèmes:
Étant donné la fonction f: x → 2x - 2 où x est un entier. Essayez de déterminer la valeur de f (3).
Solution:
La fonction f: x → 2x - 2 peut être représentée par f (x) = 2x - 2
donc,
f (x) = 2x - 2
f (3) = 2 (3) - 2 = 4
Voilà donc un exemple de relations et de fonctions en mathématiques. Avez-vous des questions à ce sujet? Veuillez noter votre question dans la colonne des commentaires et n'oubliez pas de partager ces connaissances.









