Avez-vous déjà vu le mouvement d'un pendule ou d'un ressort? Les deux mouvements que vous observez sont classés comme de simples mouvements harmoniques. C'est un mouvement de va-et-vient autour du point d'équilibre. Si vous faites attention, le pendule a un point d'équilibre au milieu, car même si sa vitesse diminue, le pendule se déplacera toujours autour du point d'équilibre.
Le mouvement harmonique simple a une amplitude (écart maximum) et une fréquence fixes. Ce mouvement est périodique. Chaque mouvement se produira à plusieurs reprises et régulièrement au même intervalle de temps.
En mouvement harmonique simple, la force résultante a la même direction, à savoir vers le point d'équilibre. Cette force est appelée la force de restauration. La quantité de force de restauration est directement proportionnelle à la position de l'objet vers le point d'équilibre.
Certaines des caractéristiques de ce mouvement comprennent un graphique de la position des particules en fonction du temps sous la forme d'un sinus ou d'un cosinus. Ce mouvement peut également être vu à partir de l'équation de la déviation, de l'équation de la vitesse, de l'équation de la vitesse et de l'équation énergétique du mouvement en question.
(Lire aussi: Quantités dans le concept de mouvement rectiligne)
Sur la base de ces caractéristiques, un mouvement harmonique simple a une déviation, une vitesse, une accélération et une énergie.
Déviation
Une simple déviation harmonique peut être considérée comme la projection de particules se déplaçant en cercles réguliers sur le diamètre du cercle. En général, l'équation de déviation dans ce mouvement est la suivante.
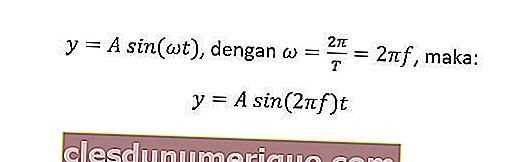
y = écart des vibrations (m)
ω = vitesse angulaire (rad / s)
T = période (s)
f = fréquence (Hz)
t = temps (s) de déplacement
A = amplitude / écart maximum (m)
La vitesse
La vitesse est la première dérivée de la position. Dans un mouvement harmonique simple, la vitesse est obtenue à partir de la première dérivée de l'équation de déviation. L'équation de vitesse peut être décrite comme suit.

Accélération
L'accélération d'un objet mobile harmonique simple peut être obtenue à partir de la première dérivée de l'équation de vitesse ou de la deuxième dérivée de l'équation de déviation. L'équation d'accélération peut être obtenue comme suit.
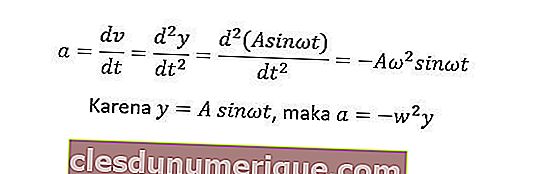
La déviation maximale a une valeur égale à l'amplitude (y = A), donc l'accélération maximale est am = - Aw
Énergie
L'équation d'énergie dans un mouvement harmonique simple comprend l'énergie cinétique, l'énergie potentielle et l'énergie mécanique. L'énergie cinétique de l'objet peut être formulée comme suit.
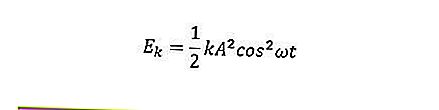
L'énergie potentielle de l'objet peut être formulée comme suit.
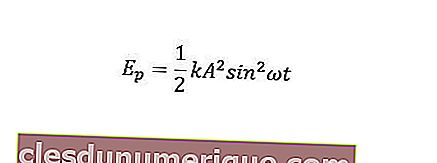
Pendant ce temps, l'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle.
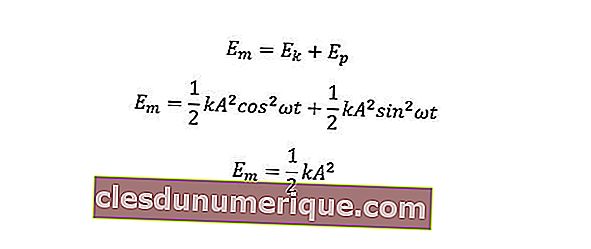
k = valeur fixe (N / m)
ω = vitesse angulaire (rad / s)
A = amplitude (m)
t = temps (s) de déplacement
La quantité d'énergie potentielle et d'énergie cinétique d'un objet déplaçant des harmoniques simples est toujours fixe.









